I’ve recently applied to Toptal and sucked miserably at the entry exam. My algo chops were blunt and I thought I’d rectify it by revisiting Project Euler. With the startup last year and the baby this year I just haven’t been able to find the time for programming challenges, but that has to change.

Looking at my Project Euler source directory, I saw that I left it at problem 17, so next up will be 18. The problem description, however, mentions that the problem repeats itselt as 67, but with a bigger input that will run 20 billion years if you go the brute force route.

I worked a little on this problem last night, and decided to by-pass the brute force solution completely. It was a bit late, though, and I pulled my eyelids open far enough to make it to bed. I then went on to dream about the damn problem all night. I knew there had to be a simple bottom-up fold-based solution, and the voila moment came for me when I realised I had to seed the fold computation with the base layer in the triangle.

Here you go:

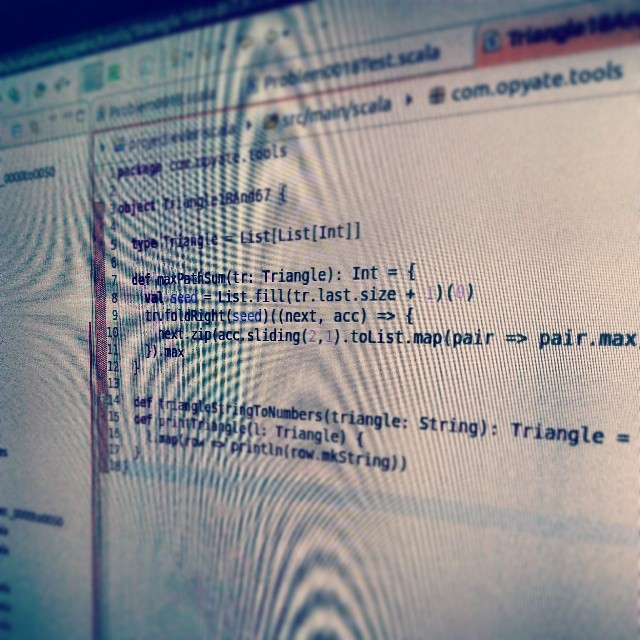
https://gist.github.com/opyate/7689573

A little explanation

The triangle is represented as a nested list, like so: List(List(1), List(2, 3), List(4, 5, 6)) and so forth.

     1
    / \
   2   3
  / \ / \
 4   5   6    <- this is the "base layer" in my explanation.

Since you need to add the maximum of the two immediate children to the layer above, a foldRight wouldn’t give me all the info I need in the curent iteration. Foldright for me means “the data is coming FROM the right”, i.e. List(4, 5, 6) will be processed first, then List(2, 3) but at no point in the iteration will they be available together so I can do the sum. List(4, 5, 6) would need to come into the iteration with List(2, 3) in another way, and I realised I can use the foldRight’s accumulator for that by seeding the foldRight with the base layer in the triangle (aka the last list List(4, 5, 6)).

The easiest way was to just seed the foldRight with a list of zeros one element larger than the base layer. You then break it up into pairs using sliding(2,1), take the max of the pairs, and sum the max with the corresponding (thanks to zip) element in the layer above.

      1
     / \
    2   3
   / \ / \
  4   5   6
 / \ / \ / \
0   0   0   0    <- this becomes the new "base layer", or "seed"

No mutable state; no recursion; simple to understand. As Erik Meijer would say: “baby code”.